之前的文章已经讲解了直接插入排序算法的过程,当时也指出了直接插入排序存在的问题:每插入一个元素都需要进行大量的移动操作,这导致这种算法的性能不算高。既然原因已经找到了,其它几种插入算法实际上都是针对这个问题提出了自己的优化方式。这篇文章就来讲解其中有名的一个——希尔排序。
1. 排序思路
我们先”随意“找一个间隔(gap),对待排序的数列按这个间隔取数,这会从原数列中筛选出一个新的数列,我们对这个新的数列执行直接插入排序。然后,我们再找一个比之前间隔略小的一个间隔(gap-2),把上面这个过程再来一遍,…. 最后,我们将这个间隔取成1(gap-n = 1),仍然进行一次上面的过程,这样便排序完成。
希尔排序的算法思路大概如此,只用文字描述可能不够直观,下面结合例子和图解来详细说说这个过程。
2. 图解排序过程
正式开始前我们先给出一个间隔列:[701, 301, 132, 57, 23, 10, 4, 1]。我们暂时先不纠结这个间隔列是怎么来的,这并不妨碍我们使用它。
接下来要准备一个例子,我们随手写下一个数字列:[0, 5, 3, 2, 2, 8],把它作为我们这个过程的主角。现在我们的任务是:借助间隔列将希尔排序算法作用于此数字列,以达到排序之目的。
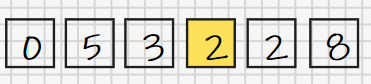
首先,我们从间隔列中取一个间隔,但这里只有6个数字,所以可用的间隔只有4和1,毕竟我们没有办法从一个只有6个数字的数列中找出间隔为10(>=6)的两个数字。并且我们要先使用最大可用间隔,这里也就是gap=4。这表示我们接下来需要从原数列中每隔4个数取一个数,组成一个新的数列,也就是像下面那样做:
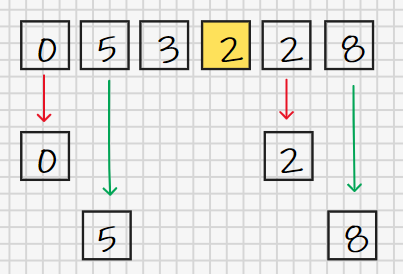
现在,我们得到两个新的数列:[0,2]和[5,8]。按照思路,我们需要对这两个数列执行直接插入排序,因为这两个数列实际上是有序的,所以我们执行完直接插入排序过程后,它们并没有什么不同。
间隔取4的情况我们已经进行完了(尽管从表面上看,我们似乎什么都没做),下面应该让间隔取1了(最后一个使用的间隔一定是1),这表示我们需要从原数列中每隔1个数取一个数,这意味着什么?我们接下来的新数列就是原数列本身:
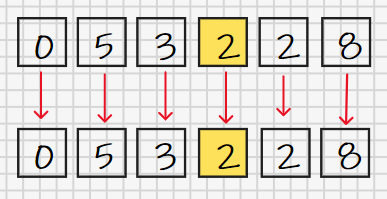
按照思路,接下来我们需要对这个新数列执行直接插入排序,这样的结果当然是整个数列变成了有序数列(升序)。
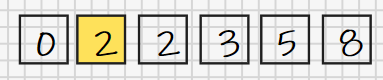
这其实说明了为什么我们无论使用怎样的间隔列,我们必须保证最后一个间隔得是1,因为只有这样我们才能在最后一次排序时至少对所有数组成的数列进行一次直接插入排序,从而保证最后得到的数列是有序的。到这里,可能有人会觉得矛盾,单从上面这个例子看,还不如一开始就对整个数列进行一次直接插入排序,一步到位,做的工作更少;另外,既然迟早会对整个数列执行一次直接插入排序,为什么还要使用间隔排序这多此一举呢?
答案在于,我们前面所进行的间隔排序会影响最后一次对整个数列的排序过程,更进一步说,前面的动作减少了最后一次排序元素时可能移动的次数。希尔排序对直接插入排序减少元素移动次数的改进也正体现在这里。从道理上理解,我们前面的每一次间隔排序都使整个数列从整体上更有序,这样当我们最后对整个数列进行直接插入排序时,往往要比一开始就使用直接插入排序所进行的工作量(移动元素)要少。
3. 间隔列
上面使用了一个凭空给出的间隔列[701, 301, 132, 57, 23, 10, 4, 1]。经过上面的分析,我们也隐隐能察觉到,如果前一次间隔排序的效果更好,那么对后一次排序直至最后一次对整个数列的排序的工作最减少都有更大的作用。没错,希尔排序性能的好坏,很大程序上取决于使用一组怎样的间隔列,很不幸的是,计算不出一个这样的间隔列,它在给任何数列排序时都能达到最佳效果。
那么,退而求其次,目前为止,有一些效佳的间隔列供我们使用,比如上面我们所使用的 [701, 301, 132, 57, 23, 10, 4, 1] 。这是 Marcin Ciura 在Best Increments for the Average Case of Shellsort一文中提出的一种较佳的希尔排序间隔列策略,这是一个经验间隔列,这表示,没法用一个明确的公式来概括它,这样当我们待排序的数列有10000个元素时,就需要找到10000内的那个最大可用间隔,这显然不太方便。另一个是大家可能听说过的是Knuth’s sequence,用公式表示为(3^k-1)/2,这代表了这样一组间隔[..., 1093, 364, 121, 40, 13 ,4, 1]。
这当然不是间隔列的全部故事,正如维基百科Shellsort条目中的一段话:
The question of deciding which gap sequence to use is difficult. Every gap sequence that contains 1 yields a correct sort (as this makes the final pass an ordinary insertion sort); however, the properties of thus obtained versions of Shellsort may be very different. Too few gaps slows down the passes, and too many gaps produces an overhead.
引自 https://en.wikipedia.org/wiki/Shellsort#Gap_sequences
那里也列出了迄今为止,人们所探索的大多数可用间隔列。
4. 代码实现
def shell_sort(collection):
gaps = [701, 301, 132, 57, 23, 10, 4, 1]
for gap in gaps:
for i in range(gap, len(collection)):
insert_value = collection[i]
print(insert_value)
j = i
while j >= gap and collection[j-gap] > insert_value:
collection[j] = collection[j-gap]
j -= gap
if j != i:
collection[j] = insert_value
return collection
if __name__ == "__main__":
print(*shell_sort([0, 5, 3, 2, 2, 8]))#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Marcin Ciura's gap sequence
const vector<int> gaps({ 701, 301, 132, 57, 23, 10, 4, 1 });
void shell_sort(vector<int>& ivec) {
auto feat_gap = find_if(gaps.cbegin(), gaps.cend(),
[&](auto gap) { return gap < ivec.size(); });
for (auto gap_iter = feat_gap; gap_iter != gaps.cend(); ++gap_iter) {
for (int i = *gap_iter; i < ivec.size(); ++i) {
int insert_value = ivec.at(i);
int j = i;
while (j >= *gap_iter && ivec.at(j - *gap_iter) > insert_value) {
ivec[j] = ivec.at(j - *gap_iter);
j -= *gap_iter;
}
if (j != i)
ivec[j] = insert_value;
}
}
}
int main() {
//vector<int> nums({ 0, 5, 3, 2, 2, 8 });
vector<int> nums({ 3, 6, 1, 4, 8, 2 });
shell_sort(nums);
for(auto n : nums)
cout << n << ", ";
}从代码中可以看出,内层for是直接插入排序的过程,而外层for控制着每次所生成数列使用之间隔。
5. 参考
Fastest gap sequence for shell sort?