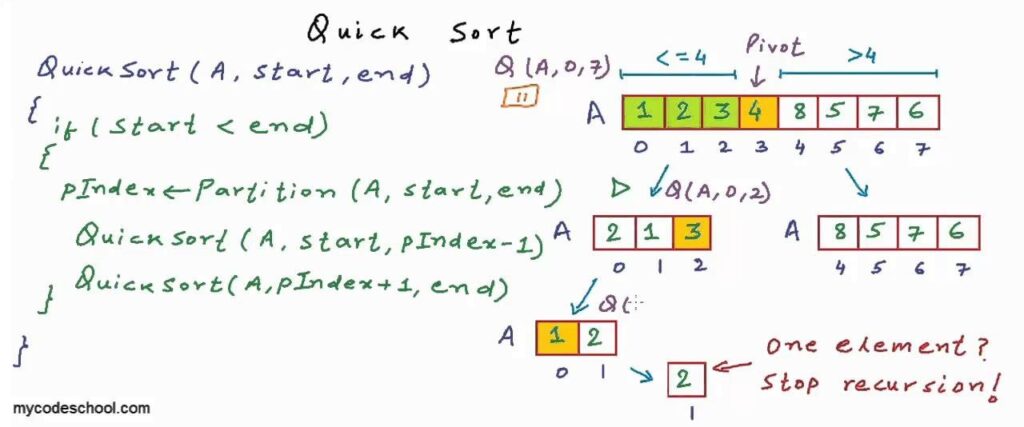
快排通常是一中非常高效的排序算法,并且其常规实现也非常简单,往往很容易理解其思路并写出实现码,前提是需要解决递归这种思考方式。
1. 排序思路
开始的时候,我们从整个数列中“任意”找出一个数作为基准数(pivot),接着拿剩余的数挨个与这个基准数比较,比它小的放在它左边,比它大的放在它右边,这便完成了一次划分(partition)。结果是我们把原来的整个数列以基准数为中点分成了两个子数列(当把子数列当成一个整体的时候,此时整个序列是有序的)。接下来要对这两个子数列做的事情和刚刚对整个数列做的事情一样……一直到子数列只有一个数的时候,自然成序,整个数列也在这一次次划分动作中完成排序。
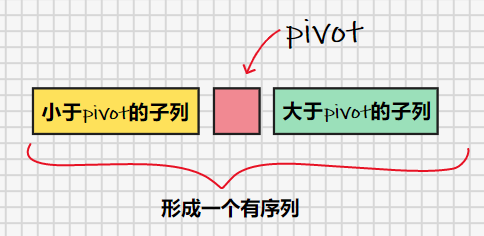
再具体一点描述的话:“对整个数列施行一次划分,把小于pivot的子列看成一个新的数列,回到这句话的开头,把大于pivot的子列看成一个新的数列,回到这句话的开头”。如果大家在认真读这句话的话,你至少是读不到当前这句话的,它是读不完的。从程序的角度看,这陷入了无穷递归,最终导航到stackoverflow(.com)。从上面的描述中,我们发现是有一个结束点的,换句话说,当数列只剩一个数的时候,我们觉得划分这个动作的意义已经消失了,这时low_ptr==high_ptr。
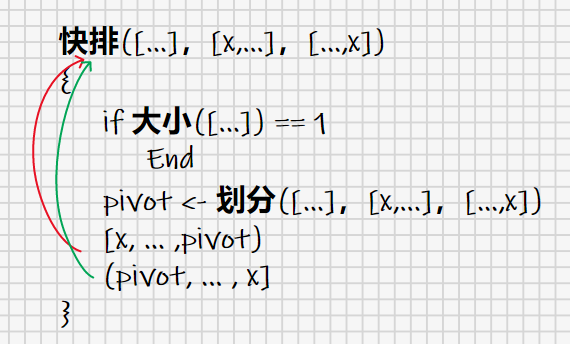
2. 图解快排过程
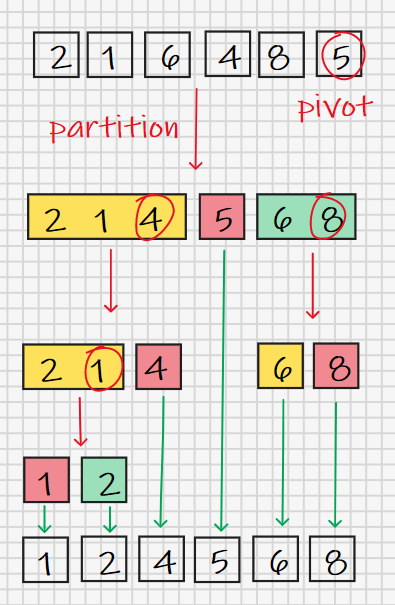
先给出一个待排序的数列[2, 1, 6, 4, 8, 5]。按照思路,我们需要从中找一个元素作为基准数,这里我们使用最后一个元素5作为基准数,至于为什么偏偏是最后一个元素,我们下面会结合算法性能再讨论。
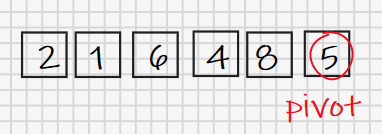
实际上,我们有两个需要图解的地方,一个是快排的递归部分,一个是划分算法部分。递归部分借助划分算法不断向下进行,直到当前待划分的数列中仅剩一个元素。递归部分更像一个执行控制流,而真正的执行由划分部分完成。
下面我们用图解的方式看看划分部分是怎样实现的,我们拿上面图解中的第一步(也就是对整个原始序列进行划分那一步)来举例。
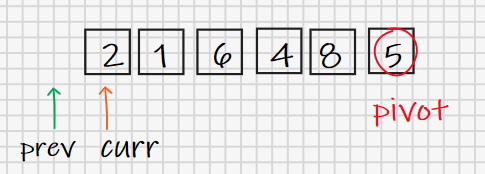
具体实现上我们借助几个变量记录索引(index)来完成比较和交换操作,prev初始为-1,这就是它在图中指向第一个元素之前的原因,它会始终记录最近一个小于pivot的值的索引;curr初始为0,也就是指向第一个元素,它会向后挨个取元素(除pivot以外),然后每拿到一个元素都会与pivot进行比较,如果小于pivot就把prev更新到这个元素处,如果大于pivot则什么也不做。
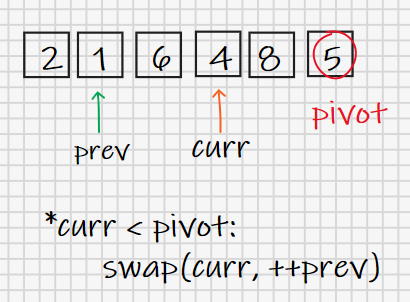
建议大家用纸笔模拟一下这个过程,结果便是划分操作的输出,随着最后一步——将pivot换到prev++的位置,pivot将数列划分成小于自己与大于自己的两个部分。
3. 基准数(Pivot)
基准数并没有什么最佳的选择方式,依旧取决于待排序数的数理性质,上面我们总是使用数列中最后一个元素作为基准数,实际上也可以总是使用第一个,或使用中间那个,再或者每次都随机选择一个。
使用不同的选择方式是为了算法性能,如果原来的数列是一个倒序的数列,再总是用最后一个元素作为基准数,性能会怎样?这个时候每次划分的结果总是n-1个元素和0个元素,并且每次划分的代价都是 Θ (元素数),所以此时算法运行时间的递归式为 T(n)=T(n−1)+Θ(n),解为T(n)=Θ(n2)。 这便是快排最坏情况下的时间复杂度。
理想情况下,选择的基准数总是能够将当前数列分成两等份,此时 算法运行时间递归式为 T(n)=2T(n/2)+Θ(n),解为T(n)=Θ(nlgn)。为了朝这个方向努力,应该结合待排序数列的数理性质来确定基准数的选择策略。另外,使用随机选择的方式至少可以极大程序的避免最坏情况的出现。
4. 代码实现
def quick_sort(collection: list) -> list:
if len(collection) < 2:
return collection
pivot = collection.pop()
greater: list[int] = []
lesser: list[int] = []
for element in collection:
(greater if element > pivot else lesser).append(element)
return quick_sort(lesser) + [pivot] + quick_sort(greater)
if __name__ == "__main__":
nums = [2, 1, 6, 4, 8, 5]
print(*quick_sort(nums))
#include <iostream>
#include <vector>
#include <random>
#include <ctime>
using namespace std;
int partition(int collection[], int low, int high) {
int prev = low - 1;
int pivot = collection[high];
for (int curr = low; curr < high; ++curr) {
if (collection[curr] < pivot) {
++prev;
swap(collection[prev], collection[curr]);
}
}
swap(collection[++prev], collection[high]);
return prev;
}
void quick_sort(int collection[], int low, int high) {
if (low < high) {
int pivot_index = partition(collection, low, high);
quick_sort(collection, low, pivot_index - 1);
quick_sort(collection, pivot_index + 1, high);
}
}
int main() {
int collection[] = { 2, 1, 6, 4, 8, 5 };
quick_sort(collection, 0, 5);
for (int i = 0; i < 6; ++i)
cout << collection[i] << ",";
}